Terceiro capítulo da série de estudos sobre o livro Entendendo Algoritmos de Aditya Y. Bhargava.

Se você está acompanhando a série, já resumi os capítulos anteriores 👀, então volta lá se tu tiver alguma dúvida:
- Capítulo 1 - Introdução a algoritmos
- Capítulo 2 - Ordenação por seleção
- Capítulo 3 - Recursão -📍 você está aqui

Oi, pessoal! Mais um resuminho do nosso livro querido 😊

Esse capítulo foi um dos que mais me tirou a sensação de que programação é mágica. Bora entender recursão e pilhas sem medo?

Neste capítulo, o autor explica de forma simples o conceito e o uso da recursão, dividindo a explicação em caso base e caso recursivo. Ele sugere que você, ao menos uma vez, analise uma função recursiva com papel e caneta, acompanhando passo a passo, assim você entenderá como a função funciona.

Recursão

É a técnica onde uma função chama a si mesma para resolver um problema, dividindo-o em problemas menores. Devido ao fato de uma função recursiva chamar a si mesma, é mais fácil de escrevê-la de forma errada e acabar em um loop infinito. Para que a recursão funcione corretamente, ela deve conter um caso base para parar as chamadas e um caso recursivo que aproxime o problema da solução final.

Como a recursão funciona:

Antes de mostrar um exemplo de recursão, vamos entender como ela funciona.

1. Caso base: define quando a função deve parar de se chamar. Sem ele, a recursão continuaria indefinidamente, causando erro.

2. Caso recursivo: é a parte em que a função se chama novamente, aproximando-se da solução final a cada passo.

Um exemplo clássico é o cálculo do fatorial de um número::

def fatorial(n):
    if n == 0 or n == 1:  # Caso Base
        return 1
    else:  # Caso Recursivo
        return n * fatorial(n - 1)

print(fatorial(5))  # Saída: 120

Nesse exemplo:

• Caso Base: n é 0 ou 1, o fatorial é 1
• Caso Recursivo: Se n é maior que 1, o fatorial é n * fatorial(n-1)

Olha como fica quase poético, cada número chama o próximo até o 1 dizer “chega, agora volta”. Aí a multiplicação acontece no caminho de volta.

Pilha

Suponha que você esteja fazendo um churrasco para os seus amigos. Você tem uma lista de afazeres em forma de uma pilha de notas adesivas. Quando você insere um item, ele é colocado no topo da pilha. Quando você lê um item, lê apenas o item do topo da pilha e ele é retirado da lista. Logo, sua lista de afazeres contém apenas duas ações: push (inserir) e pop (remover e ler).

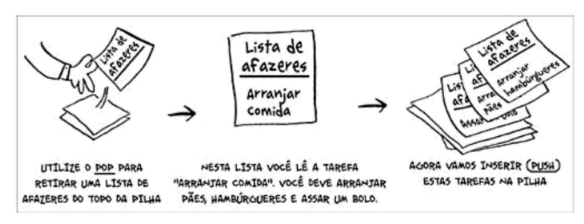
Esta estrutura de dados é chamada de pilha. A pilha é uma estrutura de dados simples e nós usamos o tempo todo sem perceber.

Pilha de chamadas

Sempre que uma função é chamada, o computador precisa “lembrar” de onde ela parou para poder continuar depois. Essa memória temporária é organizada numa pilha de chamadas (call stack).

Funciona assim:

• A cada nova chamada de função, o computador empilha informações sobre essa execução (como parâmetros e variáveis locais).
• Quando a função termina, o computador desempilha esses dados e volta para o ponto anterior.

A metáfora do livro é ótima, pense em uma pilha de pratos na cozinha. Você só consegue pegar (ou retirar) o prato que está por cima. Assim também funciona com funções, o último que entrou é o primeiro que sai (LIFO: Last In, First Out).

Podemos visualizar isso com um exemplo simples em Python:

def cumprimenta(nome):
    print("Oi,", nome)
    despedida()

def despedida():
    print("Tchau!")

cumprimenta("Ana")

Ordem de execução na pilha:

1. cumprimenta(“Ana”) é chamada → vai para a pilha.
2. Dentro dela, despedida() é chamada → fica no topo.
3. despedida() roda e sai da pilha.
4. cumprimenta(“Ana”) roda até o fim e sai da pilha.

Ou seja, tudo organizado, prato por prato.

Esse exemplo já mostra que não é só recursão que usa pilha, mas qualquer função. A diferença é que a recursão força a pilha a crescer muito mais rápido.

Pilha de chamadas com recursão

Com recursão, essa pilha pode crescer bastante, porque a função vai se chamando várias vezes até chegar no caso base.

Exemplo simplificado com fatorial(3):

O programa chama fatorial(3)
    - empilha fatorial(3)

Para resolver, precisa de fatorial(2)
    - empilha fatorial(2)

Para resolver, precisa de fatorial(1)
    - empilha fatorial(1)

fatorial(1) chega no caso base e retorna 1
    - desempilha fatorial(1)

Agora fatorial(2) consegue calcular 2 × 1 = 2
    - desempilha fatorial(2)

Por fim, fatorial(3) calcula 3 × 2 = 6
    - desempilha fatorial(3)

No fim, cada chamada só consegue terminar depois que a chamada menor retorna. É por isso que definir bem o caso base é tão importante, sem ele, a função nunca para de empilhar chamadas e acaba estourando a memória (stack overflow).

Esse “estouro da pilha” é justamente de onde veio o nome do site Stack Overflow.

Quando vi esse processo pela primeira vez, parecia uma espécie de “mágica”, como se o computador simplesmente soubesse de onde voltar.

Foi nesse momento que percebi que entender programação é muito sobre desmistificar. Não é dom, não é gênio, é só empilhar e desempilhar com calma. Hoje, sempre que vejo um código recursivo, tento imaginar essa pilha acontecendo em segundo plano, isso traz clareza e ainda transforma o “eu não nasci pra isso/nunca vou entender isso” para um “hihi que legal” 😎

Então, da próxima vez que você se perder num código recursivo, respira: desenha a pilha, segue os passos, e lembra que não é mágica, é só prática!!!

Curiosidades 💡

1. Uma recursão muito comum fora da programação: bonecas russas (matryoshkas). Cada boneca guarda outra dentro, até que a última (caso base) não guarda mais nenhuma.
2. Algumas linguagens aplicam otimização de recursão de cauda (tail call optimization), que reaproveita os quadros da pilha para não estourar a memória em funções recursivas muito profundas. Python, porém, não faz isso.
3. A pilha de chamadas é invisível na maior parte do tempo, mas você já viu ela funcionando, quando o Python mostra um traceback (aquele erro cheio de setas, indicando em que função a execução estava).
4. Muitas funções recursivas podem ser reescritas de forma iterativa (usando laços for ou while). Isso evita o risco de estouro da pilha em casos de chamadas muito profundas.
5. Para entender recursão, você precisa primeiro entender recursão. 😅

Exercícios recomendados 👩🏻‍💻💞

Para reforçar o aprendizado, aqui vão alguns desafios práticos:

LeetCode

• Merge two sorted lists - Dá pra resolver recursivamente, tratando como o caso base quando uma lista chega ao fim.
• Climbing Stairs - Um problema clássico de recursão + otimização (parecido com Fibonacci).

Exercism

• Flatten Array - Recebe uma lista que pode conter sublistas e precisa retornar tudo “achatado” em uma única lista
• Recursão com Python - Reforça o conceito de recursão e tem o exercício “Luhn” que admite uma abordagem recursiva

Desafio extra

• Crie uma função recursiva que percorre pastas e arquivos no seu computador (ou só numa lista aninhada simulada). Isso é literalmente como muitos sistemas de arquivos funcionam.

Espero que tenha aproveitado o conteúdo! ✨💕

Se tiver alguma sugestão de exercício ou melhoria na explicação, me conta aqui 🫂🌻

Compartilhar: