Segundo capítulo da série de estudos sobre o livro Entendendo Algoritmos de Aditya Y. Bhargava.

• Capítulo 1 - Introdução e Busca Binária
• Capítulo 2 - Arrays, Listas e Ordenação por Seleção -📍 você está aqui
• Capítulo 3 - Recursão

Espero que vocês tenham gostado da forma como estruturei o primeiro capítulo, seguirei naquela mesma linha de raciocínio e explicação. Se você tiver alguma sugestão de exercício ou melhoria na explicação, me conta aqui que eu ficarei feliz em receber esse feedback 🫂💕

No capítulo 2, o autor aprofunda dois conceitos fundamentais: estruturas de dados (como arrays e listas) e a eficiência dos algoritmos (notação Big O). Para ilustrar isso, ele apresenta o algoritmo de ordenação por seleção.

Arrays e Listas

Antes de falar em ordenação, é importante entender como os dados podem ser armazenados na memória. 👀

O autor traz uma analogia que faz o entendimento ficar muuuito mais fácil. Em resumo, a ideia é algo assim:

Imagine que você vai a um show e precisa guardar suas coisas na chapelaria (eu nem sabia que isso existia 🤔). Apenas algumas gavetas estão disponíveis e você pode guardar um item por gaveta. Você pega e guarda suas coisas nessas gavetas, fecha, e está pronto para ir ao show.

A memória do computador funciona mais ou menos assim. O computador parece um grande conjunto de gavetas, e cada gaveta tem um endereço. Cada vez que tu armazena um item na memória, o computador fornece um endereço para guardar esse item.

E aí, se tu quiser armazenar múltiplos itens, existem duas maneiras principais de fazer isso: arrays e listas.

Arrays

• São blocos contíguos de memória (um ao lado do outro).
• Cada elemento pode ser acessado diretamente pelo índice, permitindo uma leitura rápida.
  • Isso significa que a operação de busca por posição é O(1), ou seja, constante.

arr = [10, 20, 30]
print(arr[1])  # acesso direto ao 20

• O lado ruim do array é que, se tu quiser adicionar mais um item e a gaveta seguinte estiver ocupada, será necessário solicitar ao computador uma área de memória maior para armazenar todos os itens e mover os existentes para lá.
• Então adicionar novos itens a um array é algo que pode ser muito lento.
• Deletar um elemento é tão custoso quanto adicionar, todos os elementos seguintes precisam ser movidos.

Listas encadeadas

• Seus itens podem estar em qualquer lugar da memória.
• Cada item armazena o endereço do próximo item da lista.
• Semelhante a uma caça ao tesouro, cada pista encontrada indica onde está a próxima etapa.
• Adicionar um item é simples, você coloca o item em qualquer lugar da memória e atualiza o endereço do item anterior.
• Para deletar, é tão simples quanto, basta alterar o endereço do item anterior para apontar para o próximo item.
• O lado ruim da lista encadeada é que, para acessar um elemento específico (por exemplo, o último), você não pode ir direto, precisa percorrer a lista item por item até chegar lá.

  class Node:
      def __init__(self, valor):
          self.valor = valor
          self.proximo = None

  a = Node(10)
  b = Node(20)
  a.proximo = b

  # Percorrendo
  n = a
  while n:
      print(n.valor)
      n = n.proximo

Explicando o código acima: 1. Crio a classe Node, que armazena um valor (valor) e um ponteiro para o próximo nó (proximo). 2. Crio dois nós: a com valor 10 e b com valor 20. 3. Ligo a ao b com a.proximo = b. 4. Percorro a lista com while n: imprimindo n.valor até chegar no final (None).

A saída pra esse código:

10
20

Não sei vocês, mas entender a diferença entre arrays e listas foi um verdadeiro estalo para mim. Como aprendi Python primeiro, eu meio que usava essas estruturas no automático… 🥲 Pode parecer algo óbvio ou até desnecessário, afinal, lidamos com arrays e listas o tempo todo, mas foi incrível compreender por que as coisas funcionam do jeito que funcionam. Minha cabeça finalmente começou a encaixar as peças e perceber a lógica por trás das operações. Fiquei meio que:

Aqui estão os tempos de execução para as operações mais comuns em arrays e listas encadeadas

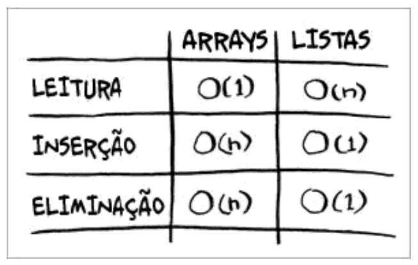
Acho importante trazer essa tabela, para que o entendimento sobre notação Big O se consolide e pra todos entenderem o impacto das nossas escolhas em diferentes situações.

A interpretação pra essa tabela de uma forma mais explícita seria:

• Leitura:

  • Array → O(1): Em um array, cada posição tem um endereço fixo na memória. Então, se você quiser o 5º elemento, o computador vai direto nele de uma forma super rápida e em tempo constante.

  • Lista → O(n): uma lista encadeada, cada elemento sabe apenas quem é o próximo. Então, para achar o 5º elemento, você precisa começar do 1º, depois o 2º, depois o 3º… até chegar no 5º. Quanto maior a lista, mais tempo demora.

• Inserção:

  • Array → O(n): Se o array estiver cheio e você quiser enfiar um novo item no meio, tem que “empurrar” todos os outros elementos uma posição para frente. Isso pode levar bastante tempo.

  • Lista → O(1): Se você já sabe a posição, inserir numa lista é rapidinho, basta mudar quem aponta pra quem e pronto.

• Deleção:

  • Array → O(n): Se você remove um item no meio do array, precisa “puxar” todos os elementos da frente uma posição pra trás para fechar o buraco.

  • Lista → O(1): Assim como na inserção, basta mudar os ponteiros para pular o item que você quer remover. Não mexe em mais ninguém.

Ordenação por seleção

O autor apresenta o algoritmo Selection Sort, que é simples de implementar, mas não muito eficiente. A diferença entre arrays e listas em Python torna importante entender como o algoritmo percorre e manipula os elementos.

Ideia do algoritmo

1. Encontrar o menor elemento da lista
2. Colocá-lo na primeira posição
3. Repetir para as posições seguintes até ordenar toda a lista

Implementação em Python:

def busca_menor(arr):
    """
    Encontra o índice do menor elemento em um array.

    Parâmetros:
    arr (list): Lista de elementos comparáveis.

    Retorna:
    int: Índice do menor elemento encontrado.
    """
    menor = arr[0]
    menor_indice = 0
    for i in range(1, len(arr)):
        if arr[i] < menor:
            menor = arr[i]
            menor_indice = i
    return menor_indice

def ordenacao_por_selecao(arr):
    """
    Ordena uma lista usando o algoritmo de ordenação por seleção.

    A função cria uma nova lista, removendo o menor elemento
    da lista original a cada iteração e adicionando-o à lista ordenada.

    Parâmetros:
    arr (list): Lista de números a serem ordenados.

    Retorna:
    list: Nova lista ordenada em ordem crescente.
    """
    novo_arr = []
    for i in range(len(arr)):
        menor = busca_menor(arr)
        novo_arr.append(arr.pop(menor))
    return novo_arr

print(ordenacao_por_selecao([5, 3, 6, 2, 10])) # Saída: [2, 3, 5, 6, 10]

Complexidade e Big O

• O selection sort precisa percorrer todos os elementos várias vezes.
• Para n elementos, ele faz aproximadamente n × n operações.
• Isso significa que seu desempenho é O(n²).

Este é um exemplo clássico que mostra como algoritmos diferentes podem resolver o mesmo problema com eficiências diferentes, destacando a importância de escolher o algoritmo certo dependendo do tamanho e da estrutura dos dados.

Curiosidades

• As listas em Python são, na verdade, arrays.
• O método append (adicionar no final) é considerado de complexidade O(1) na média. Isso porque adicionar um item no final geralmente é bem barato: só colocar no próximo espaço livre.
• O “custo alto” aparece em operações como insert ou remove no meio da lista. Aí é preciso deslocar todos os elementos seguintes, o que pode ser O(n).
• Uma forma de visualizar: pense numa pilha de pratos. Colocar ou tirar um prato do topo (como append e pop) é fácil. Mas se você quiser enfiar ou tirar um prato do meio da pilha (insert ou remove), vai ter que mover todos os pratos que estavam em cima primeiro.

Exercícios recomendados 👩🏻‍💻💞

Para reforçar o aprendizado, aqui vão alguns desafios práticos:

LeetCode

• Two Sum - clássico de arrays

• Best Time to Buy and Sell Stock - Percorrer array com análise de tempo

• Merge Sorted Array - Manipulação de listas ordenadas

Exercism

• Isogram - Percorre strings/arrays verificando duplicatas

E assim, fechamos o segundo capítulo! Espero que tenha sido útil e leve de ler 💁🏻‍♀️✨

Compartilhar: